| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- CA
- codeit
- 스프링장점
- 책평가
- 스프링부트개발
- 제품증정 #에스트라 #에스트라퓨처랩서포터즈 #리제덤아이세럼 #더마아이세럼 #레티노이드아이세럼
- 말하기시험
- 컴퓨터공학
- 코멘토취업
- 컴퓨터구조
- 개발자
- 나는주니어개발자다
- 방학
- 컴퓨터공학과
- Python
- MIPS
- 코멘토5주인턴
- .env파일
- 졸업영어
- 맥북FaceID
- JS
- 소프트웨어
- 개발
- computerarchitecture
- 컴퓨터구조개념
- 함꼐자라기
- 코드잇파이썬
- 백엔드
- 파이썬
- 코드잇
- Today
- Total
sollog
DM 02 본문
TODAY’S QUESTION
Is Propositional Logic Not Enough?
명제논리로는 충분하지 않습니까?
What are quantifiers and how to use them?
P ROPOSITIONAL LOGIC NOT ENOUGH <삼단논법>
If we have: (the Socrates Example)
“All men are mortal.”
“Socrates is a man.”
Does it follow that
“Socrates is mortal?”
No.
Can’t be represented in propositional logic.
Need a language that talks about objects, their properties, and their relations.
Later we’ll see how to draw inferences.
Features
Variables: 𝑥, 𝑦, 𝑧
Predicates: 𝑃(𝑥), 𝑀(𝑥) (서술어)
Quantifiers (to be covered in a few slides):
Propositional functions
generalization of propositions
They contain variables and a predicate, e.g., 𝑃(𝑥)
Variables can be replaced by elements from their domain
Propositional functions // 명제 함수
become propositions (and have truth values) when their variables are each replaced by a value from the domain (or bound by a quantifier, as we will see later).
The statement 𝑃(𝑥) is said to be the value of the propositional function 𝑃 at 𝑥.
Ex)
let 𝑃(𝑥) denote “𝑥 > 0” and the domain be the integers
– P(-3) is False.
– P(0) is False.
– P(3) is True.
– Often the domain is denoted by U. So in this example U is the integers.
Propositional functions
Ex) Let “x+ y= z” be denoted by R(x,y,z) Find these truth values:
– R(2,-1,5) is □. False
– R(3,4,7) is □. True
– R(x , 3, z ) is □. we don’t know
Ex) Now let “x- y= z” be denoted by Q Find these truth values:
– Q(2,-1,3) is □. true
– Q(3,4,7) is □. false
– Q(x,3,z) is □. we don’t know
Compound Expressions
If 𝑃(𝑥) denotes “𝑥 > 0,” find these truth values: – 𝑃(3) ∨ 𝑃(−1) Solution: T
– 𝑃(3) ∧ 𝑃(−1) Solution: F
– 𝑃(3) → 𝑃(−1) Solution: F
– 𝑃(3) → ¬𝑃(−1) Solution: T
Expressions with variables are not propositions and therefore do not have truth values.
– 𝑃(3) ∧ 𝑃(𝑦)
– 𝑃(𝑥) → 𝑃(𝑦)
– When used with quantifiers (to be introduced next), these expressions (propositional functions) become propositions. 😮
Quantifiers
How to express “all” and “some”
– “All students are precious.”
– “Some students do not know that.”



*even : 짝수를 나타냄.

domain 영역이 유한하다고 (정해져있는 숫자) 가정하고,

** special

//Quantifiers의 우선순위

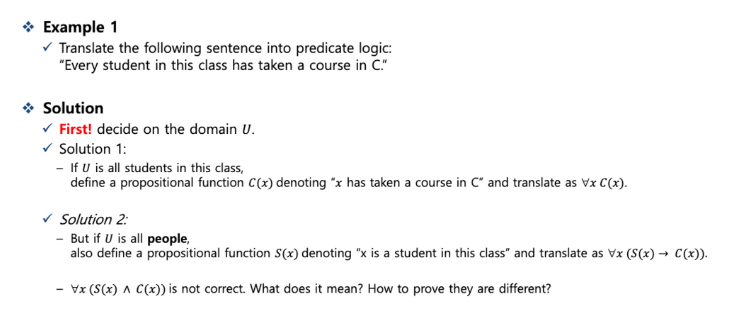
예시 1 / 해결책 solution
first . 전체 도메인 U를 결정한다.
solutions 1 .
- 만약 이 반의 모든 학생을 U라고 하면,
C(x) 는 “x has taken a course C” 의 propositional function이라고 정의내리고, 다음 기호와 같이 번역할 수 있다.
solutions 2.
그러나 만약 모든 사람들을 U 라고 하면,
또한 S(x)로 “x is a student in this class “ 로 정의내리고, 다음 기호와 같이 번역할 수 있다.

예시 2 / 해결책 solution
Solution1:
우선, 이 수업의 모든 학생들을 U라고 하면,
다음과 같은 기호로 번역할 수 있다.
Solution2: 그러나 만약 모든 사람들이 U라면,
~~

소크라테스의 예시를 들어보자.
Mortal(x)는 “x is a mortal” 이라고 나타낸다.
전제:
모든 남자는 Mortal이다.
Man(소크라테스)
결론
Mortal (Socrates)
Equivalences in Predicate Logic // 술어 논리의 동치
Statements involving predicates and quantifiers are logically equivalent if and only if they have the same truth value
notation 𝑆 ≡ T
- Conjunctions(그리고 ) / Disjunctions (또한)

모든 P(x)의 경우 = 그리고 AND 로 연결
어떤 하나의 P(x)의 경우 = 또는 OR 로 연결

표현된 식을 부정하기
The rules for negating quantifiers are:


*addictive 더했을 때 상쇄가 되는

Define P(x,y) : x * y = 0 의경우

Define P(x,y) : x / y = 1 의경우




'자기계발 > Study' 카테고리의 다른 글
| [MIPS] QtSpim - Assembly Languages (0) | 2023.10.12 |
|---|---|
| Instruction Set Completeness (2) | 2023.10.10 |
| DM 01 (0) | 2023.09.25 |
| Computer Architecture_Adressing mode (0) | 2023.09.20 |
| CA_study_1 (0) | 2023.09.19 |


