| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 스프링장점
- Git
- 컴퓨터공학과
- 코멘토취업
- 코드잇
- gitconvetion
- 개발
- 코드잇파이썬
- .env파일
- 깃충돌
- MIPS
- 컴공
- computerarchitecture
- 파이썬
- 방학
- 졸업영어
- codeit
- CA
- 깃컨벤션
- 백엔드
- JS
- 코멘토5주인턴
- 말하기시험
- 스프링부트개발
- 컴퓨터공학
- 개발자
- 제품증정 #에스트라 #에스트라퓨처랩서포터즈 #리제덤아이세럼 #더마아이세럼 #레티노이드아이세럼
- 소프트웨어
- Python
- 컴퓨터구조
- Today
- Total
sollog
DM 01 본문
1주차 2차시 수업
Course Introduction Ch. 1. The Foundations: Logic and Proofs
A proposition is a declarative sentence that is either true or false.
Practice
Discrete Mathematics
– The Moon is made of green cheese.
– Trenton is the capital of New Jersey.
– Toronto is the capital of Canada.
– 1 + 0 = 1
– 0 + 0 = 2
– Sit down!
– What time is it?
– 𝑥 + 1 = 2
– 𝑥 + 𝑦 = 𝑧
Constructing Propositions
The proposition that is always true is denoted by 𝑇 and the proposition that is always false is denoted by 𝐹.
Compound Propositions; constructed from logical connectives and other propositions
1. Negation ¬ / 부정
2. Conjunction ∧ / 그리고 (AND)
3. Disjunction ∨ / 또한 (OR)
4. Implication → / 조건문 if 만약 ~ 이면, ~ 이다 .
5. Biconditional ↔ / 상호 조건적인 only if 등
1. Negation 부정
if 𝑝 denotes “The earth is round.”,
then ¬𝑝 denotes “It is not the case that the earth is round,”
or more simply “The earth is not round.”

2. Conjunction 접속사
Ex) If 𝑝 denotes “I am at home.” and 𝑞 denotes “It is raining.”
then 𝑝 ∧ 𝑞 denotes “I am at home, and it is raining.”
AND 라서 그리고 를 나타내고, 둘 다 T 여야 조건 두개에 맞는 결과값이 T 고, 나머지는 다 F이다.

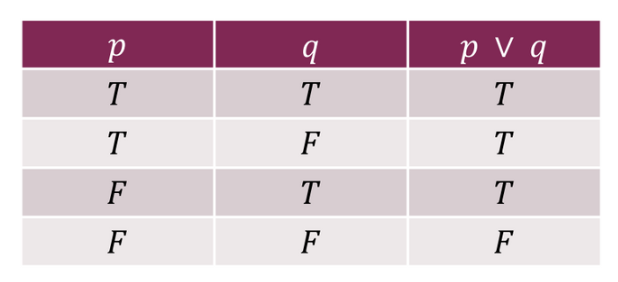
3. Disjunction 역행
Ex) If 𝑝 denotes “This is too easy.” and 𝑞 denotes “You are so smart.” then 𝑝 ∨ 𝑞 denotes “This is too easy, or you are so smart.”
OR 이라서 또한 을 나타내고, 하나라도 T 가 있으면 두개에 맞는 결과값이 T이고, 둘 다 F 일 때 조건 하나는 F 이다.
- Exclusive OR (XOR)
In 𝑝 ⊕ 𝑞, one of 𝑝 and 𝑞 must be true, but not both

- NOR이랑 헷갈리지 말자.
얘네는 두 조건이 서로 달라야 T 인 것이다. 둘 다 상태가 같으면 F 야.
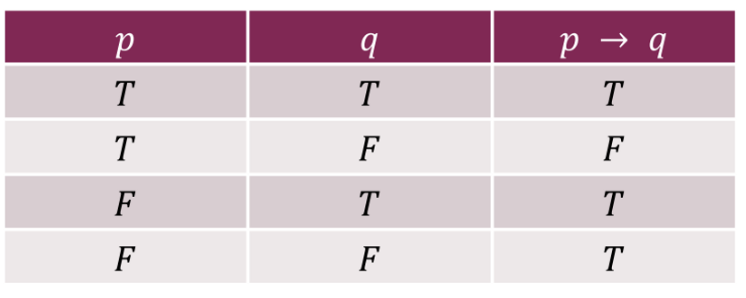
4. Implication (or conditional statement) 조건문
Ex) If 𝑝 denotes “I am at home.” and 𝑞 denotes “It is raining.” then 𝑝 → 𝑞 denotes “If I am at home then it is raining.”
In 𝑝 → 𝑞, 𝑝 is the hypothesis 가설 (antecedentor 선행의 premise 전제) and 𝑞 is the conclusion(or consequence).
Ex) “If I am elected, then I will lower taxes.” / 만약 내가 당선이 되면, 세금을 적게 내 – What if the politician who is elected does not lower texes?
– 𝑝 is true and 𝑞 is false
“If you get 100 points on the final, then you will get an A.”
당선이 됐을 경우, 세금을 적게 내고 안 내고는 사실일수도, 사실이 아닐 수도 있음
하지만 당선이 안될 경우는, 그냥 상관이 없으니까 사실이라고 표현하는 것임.
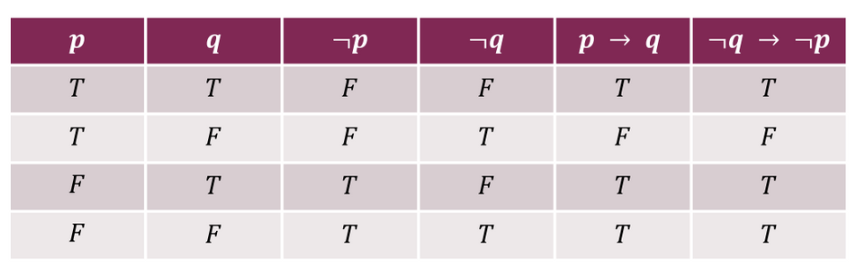
Different Ways of Expressing 𝑝 → 𝑞

Converse(역), Inverse(이), and Contrapositive(대우)
– 𝑞 → 𝑝 is the converse of 𝑝 → 𝑞
– ¬𝑝 → ¬𝑞 is the inverse of 𝑝 → 𝑞
– ¬𝑞 → ¬𝑝 is the contrapositive of 𝑝 → 𝑞
Ex) “Raining is a sufficient condition for me not to go to town.”
– converse: If I do not go to town, then it is raining.
– inverse: If it is not raining, then I will go to town.
– contrapositive: If I go to town, then it is not raining.
p is sufficient condition for q
p는 q에 충분조건이다.
p for (¬𝑞)
5. Biconditional (상호 조건문)
if and only if 𝑞.”
Ex) If p denotes “I am at home.” and q denotes “It is raining.” then 𝑝 ↔ 𝑞 denotes “I am at home if and only if it is raining.”
Alternative expressions
– 𝑝 is necessary and sufficient for 𝑞
– if 𝑝 then 𝑞, and conversely 역으로

최종 진리표

Equivalent Propositions
Two propositions are equivalent 동등한 if they always have the same truth value.
Ex) 𝑝 → q ≡ ¬𝑝 ∨ 𝑞 // Not p or q
Ex) the conditional is equivalent to the contrapositive(대우)
Precedence(우선(함), priority) of Logical Operators
p ∨ 𝑞 → ¬𝑟 is equivalent to (𝑝 ∨ 𝑞) → ¬𝑟
If the intended meaning is 𝑝 ∨ (𝑞 → ¬𝑟) then parentheses must be used.

Translating English Sentences
“If I go to Harry’s or to the country, I will not go shopping.”
– 𝑝: I go to Harry’s
– 𝑞: I go to the country.
– 𝑟: I will go shopping. – If 𝑝 or 𝑞 then not 𝑟.
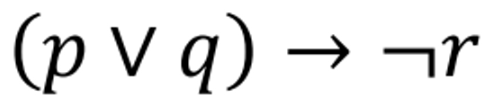
Some more – “You can access the Internet from campus only if you are a computer science major or you are not a freshman.”
– What are 𝑎, 𝑐, and f?
a: You can access the internet from campus
c: You ae a computer science major
f : you are not a freshman.
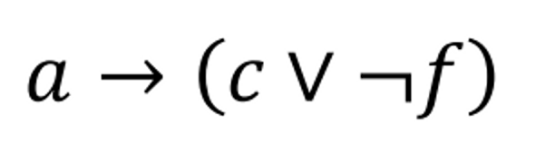
Consistent System Specifications
“The automated reply cannot be sent when the file system is full” → Let 𝑝 denote “The automated reply can be sent” and 𝑞 denote “The file system is full.”
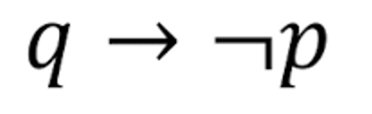
Propositional Equivalences
Tautologies, Contradictions(모순), and Contingencies(우연)
– A tautology is a proposition which is always true. » Example: 𝑝 ∨ ¬𝑝
– A contradiction is a proposition which is always false. » Example: 𝑝 ∧
¬𝑝 – A contingency is a proposition which is neither a tautology nor a contradiction, such as 𝑝

Propositional Equivalences
De Morgan’s Laws
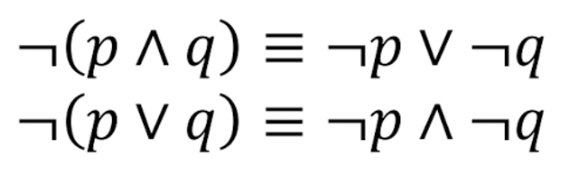

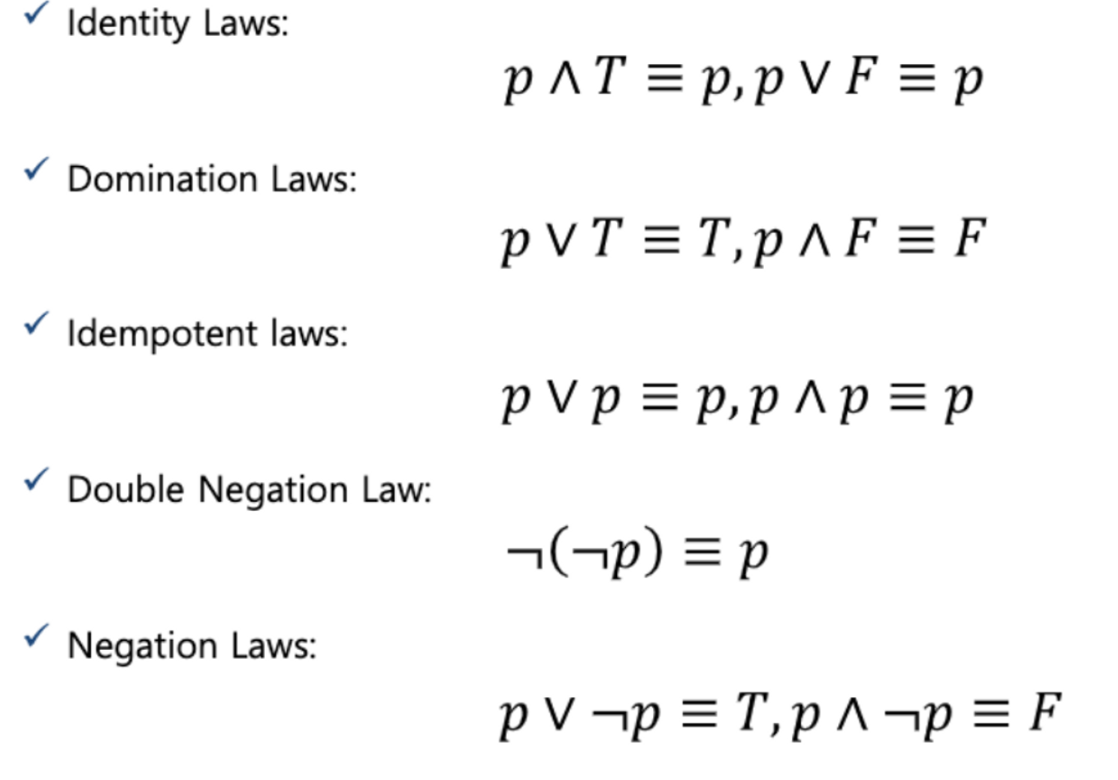
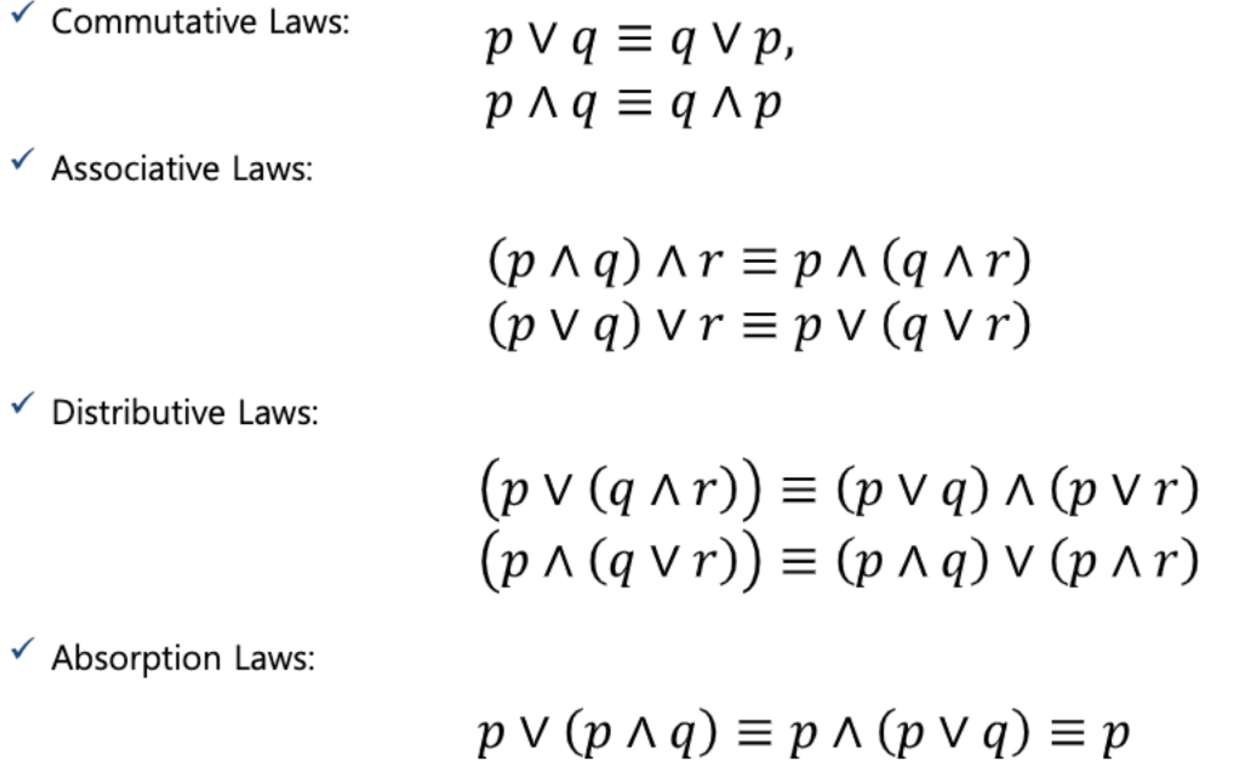

Propositional Equivalences
Involving Conditional Statements
Involving Biconditional Statements

Propositional Equivalences
Equivalence Proofs
Ex) Show that ¬ 𝑝 ∨ ¬𝑝 ∧ 𝑞 is logically equivalent to ¬𝑝 ∧ ¬𝑞 –
Solution

Propositional Equivalences
Equivalence Proofs
Ex) Show that 𝑝 ∧ 𝑞 → 𝑝 ∨ 𝑞 is a tautology.
– Solution

Satisfiability
A compound proposition is satisfiable if there is an assignment of truth values to its variables that make the compound proposition true.
When no such assignments exist, the compound proposition is unsatisfiable.
A compound proposition is unsatisfiable if and only if its negation is a tautology.
Ex)

Some more Notation (표기법)
(Multiple OR)
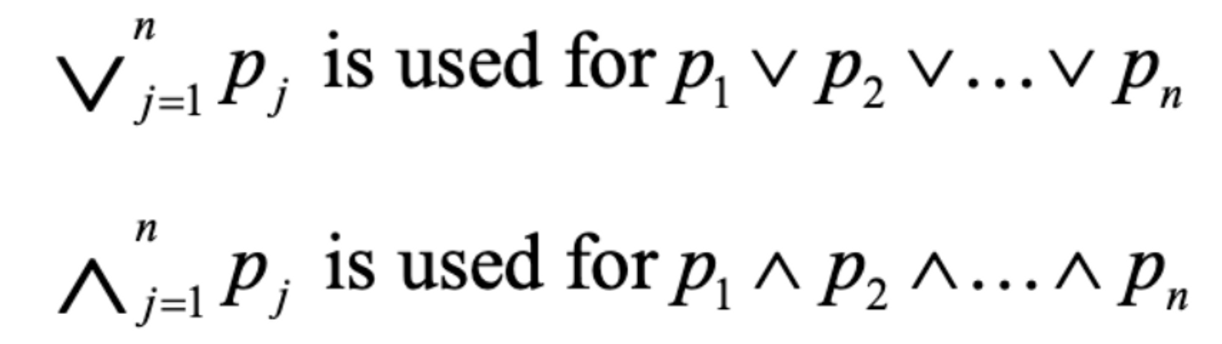

'자기계발 > Study' 카테고리의 다른 글
| [MIPS] QtSpim - Assembly Languages (0) | 2023.10.12 |
|---|---|
| Instruction Set Completeness (2) | 2023.10.10 |
| DM 02 (0) | 2023.09.25 |
| Computer Architecture_Adressing mode (0) | 2023.09.20 |
| CA_study_1 (0) | 2023.09.19 |




